This is probably obvious to all the IFC veterans out there, but it was a new discovery for me so I thought I would share. When I first started learning IFC it was because of infrastructure and alignments. I was under the mistaken impression that a Helmert transition spiral and an IfcSecondOrderPolynomialSpiral were the same thing (and this goes for all the other spirals as well, but easier to stick to a single example). I have since learned that a Helmert transition spiral is a specific instance of IfcSecondOrderPolynomialSpiral with very specifically defined polynomial coefficients. However, in general and IfcSecondOrderPolynomialSpiral is just some cool geometry that can be used for just about anything - including some fanciful roadside art.
To make this concept real to me, I created a small test file with an alignment having a single Helmert transition spiral and an IfcBuildingElementProxy. The built element has a representation that is an IfcSweptDiskSolid and the directrix is an IfcSecondOrderPolynomialSpiral. This is an example of the same spiral type being used in two very different ways.
Here are some screenshots from different viewers
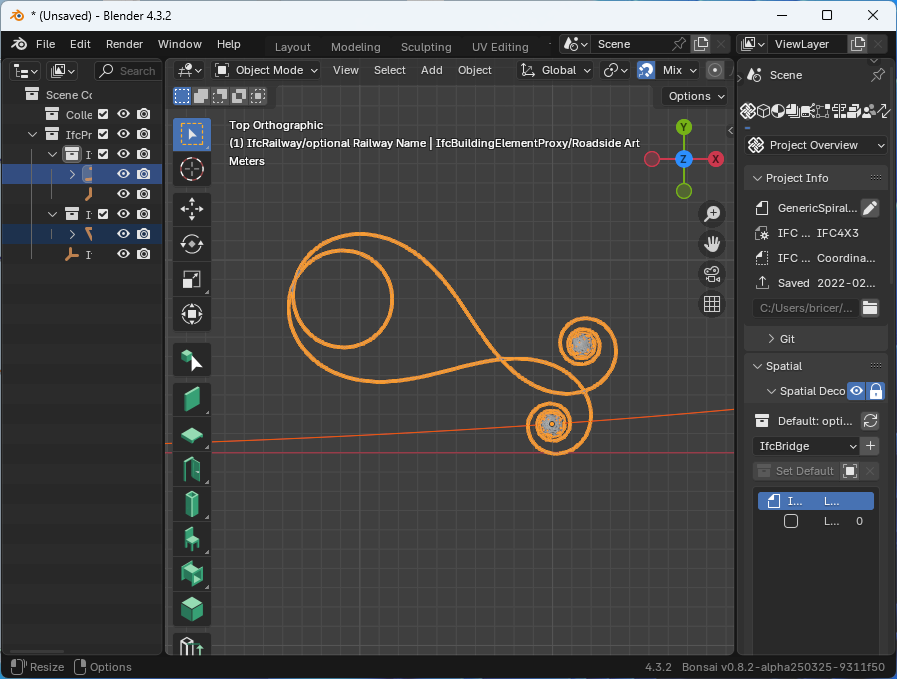
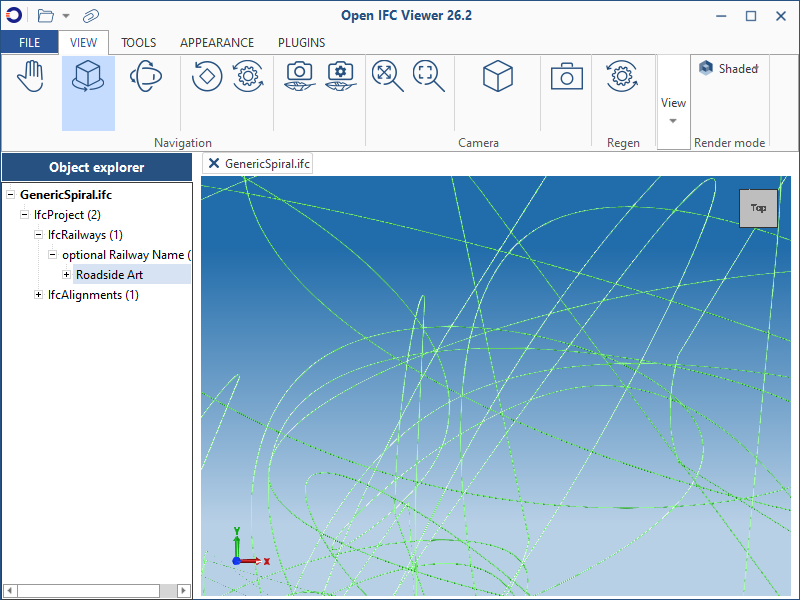

Like I say - this is probably trivial to IFC experts, but as a relative newbie, I think this is pretty cool