@paullee said:
@topologic said:
https://cardiff.zoom.us/j/83477566475?pwd=WmVwOGZxQVhQMFFaeWN3cklpSlNoQT09
Password: Topologic
Can't join / login via browser :(
And recording ?
Sorry to hear that! Yes we recorded it. Will share here in a few minutes once Zoom makes it available
Thanks for the demo Wassim.
So to go forward and add some electrical plugs to topologic I will need to go 'multidimensionaly graphed! :-)
Room and Space is already available, but on the next dimension, we would add some furniture to the room, another dimension would have the water-tap and its supply, a next dimension: the electrical-power-plug and its supply..
The power- plug can already have its roomlocation (dictionary) & positionwithintheroom (geometry = shell in the cell) (what topologic already could do). Then I need to know how I would implement the next dimension: the electrical power-supply-graph.
Would it just be a second instance of 'topologic' with an adapted behaviour (instead of geometry it would handle power ratings). Both topologic instances would run parallely and/or interact? what are the tools behind this topologic intelligence?
Is it understandable?
Lukas
@lukas said:
Thanks for the demo Wassim.
So to go forward and add some electrical plugs to topologic I will need to go 'multidimensionaly graphed! :-)
Room and Space is already available, but on the next dimension, we would add some furniture to the room, another dimension would have the water-tap and its supply, a next dimension: the electrical-power-plug and its supply..
The power- plug can already have its roomlocation (dictionary) & positionwithintheroom (geometry = shell in the cell) (what topologic already could do). Then I need to know how I would implement the next dimension: the electrical power-supply-graph.
Would it just be a second instance of 'topologic' with an adapted behaviour (instead of geometry it would handle power ratings). Both topologic instances would run parallely and/or interact? what are the tools behind this topologic intelligence?
Is it understandable?
Lukas
Thanks @lukas. The electrical power-supply-graph would be exactly that: a graph (or a wire). Both entities are well supported in Topologic and you can traverse them etc. The only hiccup is that Topologic has undirected graphs not directed ones ( @brunopostle encountered this and decided to add networkx as a plugin to analyse directed graphs). What you are describing looks to me as a set of python scripts written on top of topologic to handle domain-specific things like power ratings and network analysis etc. So you would build functionality over Topologic. All these applications are interesting to me, but to implement them, you would have to put time and effort to learn Topologic and then see how to integrate it with your goals. @brunopostle and @arquitextonica and Theo Dounas are well on their way integrating with homemaker, informational modelling, and blockchain technology respectively. Sean Fruin (Sigma Design) used it successfully for MEP/HVAC duct design (so perhaps similar to what you are describing. And finally IPRO in Germany has used it to find the rentable areas of hundreds of apartments in Revit. So it is quite versatile!
The zoom recording is available on YouTube at:
This is what I was hoping to show you at the end of the recording. A simple spatial query system. You type the names of the two rooms and it will retrieve the wall that separates them. Obviously the two rooms can have the same name. It makes no difference to Topologic.
Can we put the recording to the osarch YouTube channel or do you have your own? We'll just share it in that case.
@JanF said:
Can we put the recording to the osarch YouTube channel or do you have your own? We'll just share it in that case.
Done. I have a Topologic Tutorials Playlist on YouTube:
@topologic said:
Thanks @lukas. The electrical power-supply-graph would be exactly that: a graph (or a wire). Both entities are well supported in Topologic and you can traverse them etc. The only hiccup is that Topologic has undirected graphs not directed ones ( @brunopostle encountered this and decided to add networkx as a plugin to analyse directed graphs).
[sorry I forgot about the talk, I was cooking all afternoon]
Actually Topologic Wires work nicely as directed graphs, my only issue is that they have to be contiguous, which is difficult to control when one of the things you are trying to find out is if a set of Lines is contiguous. I did try networkx, but it didn't behave as documented (whatever I did I couldn't attach attributes to nodes), and it was unbelievably slow (0.25 seconds to add an edge to a graph), so I eventually just wrote my own mini graph library.
@brunopostle said:
@topologic said:
Thanks @lukas. The electrical power-supply-graph would be exactly that: a graph (or a wire). Both entities are well supported in Topologic and you can traverse them etc. The only hiccup is that Topologic has undirected graphs not directed ones ( @brunopostle encountered this and decided to add networkx as a plugin to analyse directed graphs).
[sorry I forgot about the talk, I was cooking all afternoon]
Actually Topologic Wires work nicely as directed graphs, my only issue is that they have to be contiguous, which is difficult to control when one of the things you are trying to find out is if a set of Lines is contiguous. I did try networkx, but it didn't behave as documented (whatever I did I couldn't attach attributes to nodes), and it was unbelievably slow (0.25 seconds to add an edge to a graph), so I eventually just wrote my own mini graph library.
Hi @brunopostle you can use a Cluster instead of Wire and self merge it . You can then ask it to return wires for the contiguous bits.
@topologic said:
@brunopostle said:]
Actually Topologic Wires work nicely as directed graphs, my only issue is that they have to be contiguous, which is difficult to control when one of the things you are trying to find out is if a set of Lines is contiguous.
Hi @brunopostle you can use a Cluster instead of Wire and self merge it . You can then ask it to return wires for the contiguous bits.
Thanks, I thought I tried that, will try again.
I deleted two comments by @ReD_CoDE since they were both condescending and rude. Since everyone else seems capable of speaking constructively I saw no reason to put up with it. This is not the first time and I had been hoping for an improvement over time.
I thought there was a way to hide rather than delete, but I can't find it...
@paullee said:
Great presentation and demonstration of what Topologic's capabailities and potential !
Too many questions from me maybe :D A few random thought -
- Since Topologic is on same engine as FreeCAD, i.e. OCCT, does it suffer the 'Topological Naming Problem'? e.g. -
- If the input geometry is changed by modifying a rectangular cell with a chamfer corner
- Would the Bathroom, originally paired up with Cell no. 3, now suddenly jump to another cells because of that problem ?
I am assuming the whole thing you demonstrate is 'parametric' (If I put it correctly with right terms)
- If ArchSpace is used in FreeCAD and attributes (like your dictionaries) are added in FreeCAD workflow, wondering would all the efforts to add information be duplicate - one in FreeCAD and one in Topologic for doing spatial analysis ?
Thanks :D
Thanks @paullee. I have heard of that problem in FC, but have not looked deeply into it. This needs testing but here are my thoughts on how this can be avoided. In Topologic you can create Cells, add Dictionaries to them and THEN build a CellComplex. If the original cells do not intersect, the dictionaries transfer 1:1. If the Cells intersect, the new Cells get a new dictionary which contains the values from both parents (e.g. “name”:[“living”,”kitchen”]) So the name of a Cell is not associated with a row number of a cell in a cell complex. There is no guarantee on the order or number of cells created in a CellComplex (eg the Topologic logo starts with two Cells, but creates three Cells when we build the CellComplex)
As to repeating effort, if and when we get to building a workbench, perhaps we do some automatic transfer of attributes from FC to Topologic Dictionaries. Could be invisible to the user.
@duncan said:
I deleted two comments by @ReD_CoDE since they were both condescending and rude. Since everyone else seems capable of speaking constructively I saw no reason to put up with it. This is not the first time and I had been hoping for an improvement over time.
I thought there was a way to hide rather than delete, but I can't find it...
I thought we agreed on using edit with the spoiler tag:
! Hidden text
deleting is appropriate first when someone is actively trolling in my opinion.
Technical hurdles with #cppyy just overcome (finally!). We will soon have #TopologicPy for #python, @Blender, #sverchok, and @FreeCADNews on #Windows10. I am still in awe of #Linux though ?.
@lukas said:
Then I need to know how I would implement the next dimension: the electrical power-supply-graph.
Would it just be a second instance of 'topologic' with an adapted behaviour (instead of geometry it would handle power ratings). Both topologic instances would run parallely and/or interact? what are the tools behind this topologic intelligence?
Hi Lukas,
I'm working with graphs as knowledge support based on key value dictionaries.
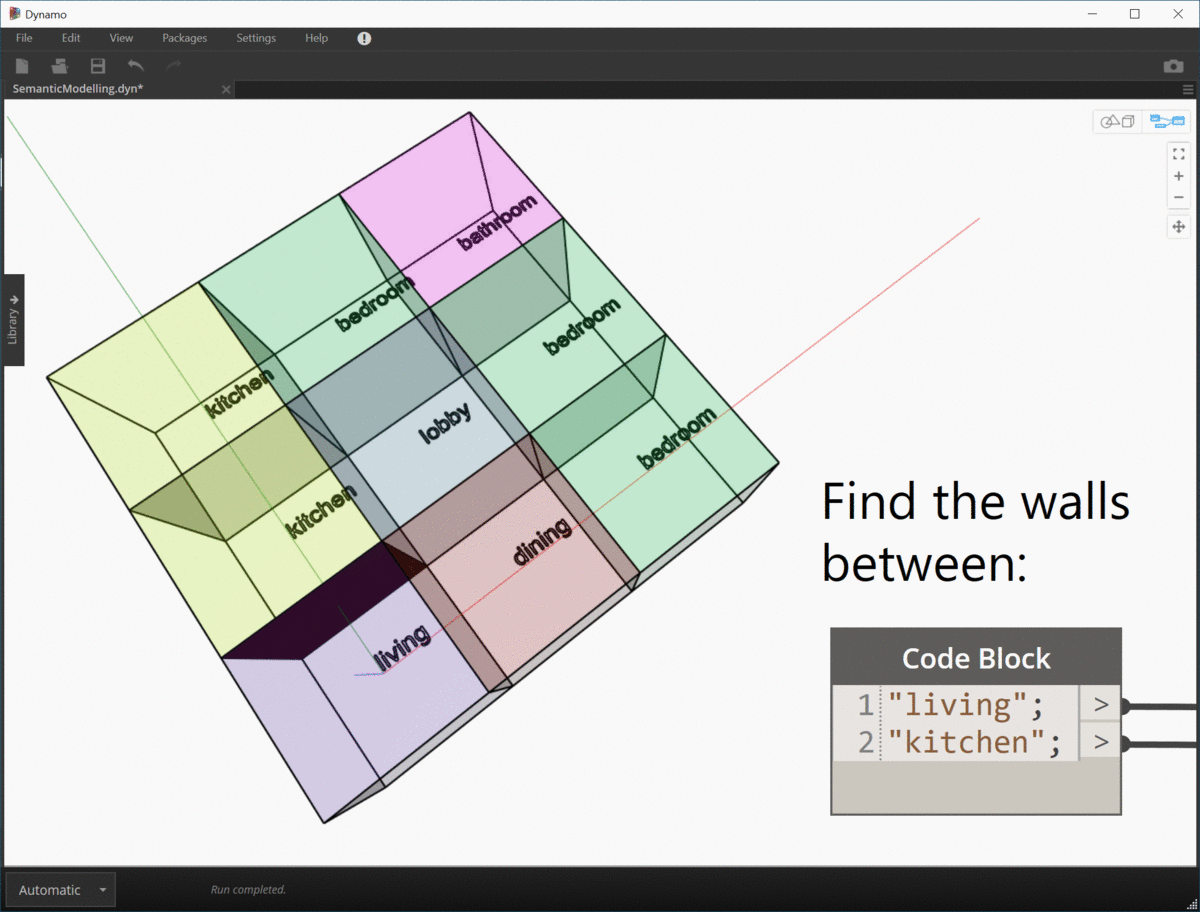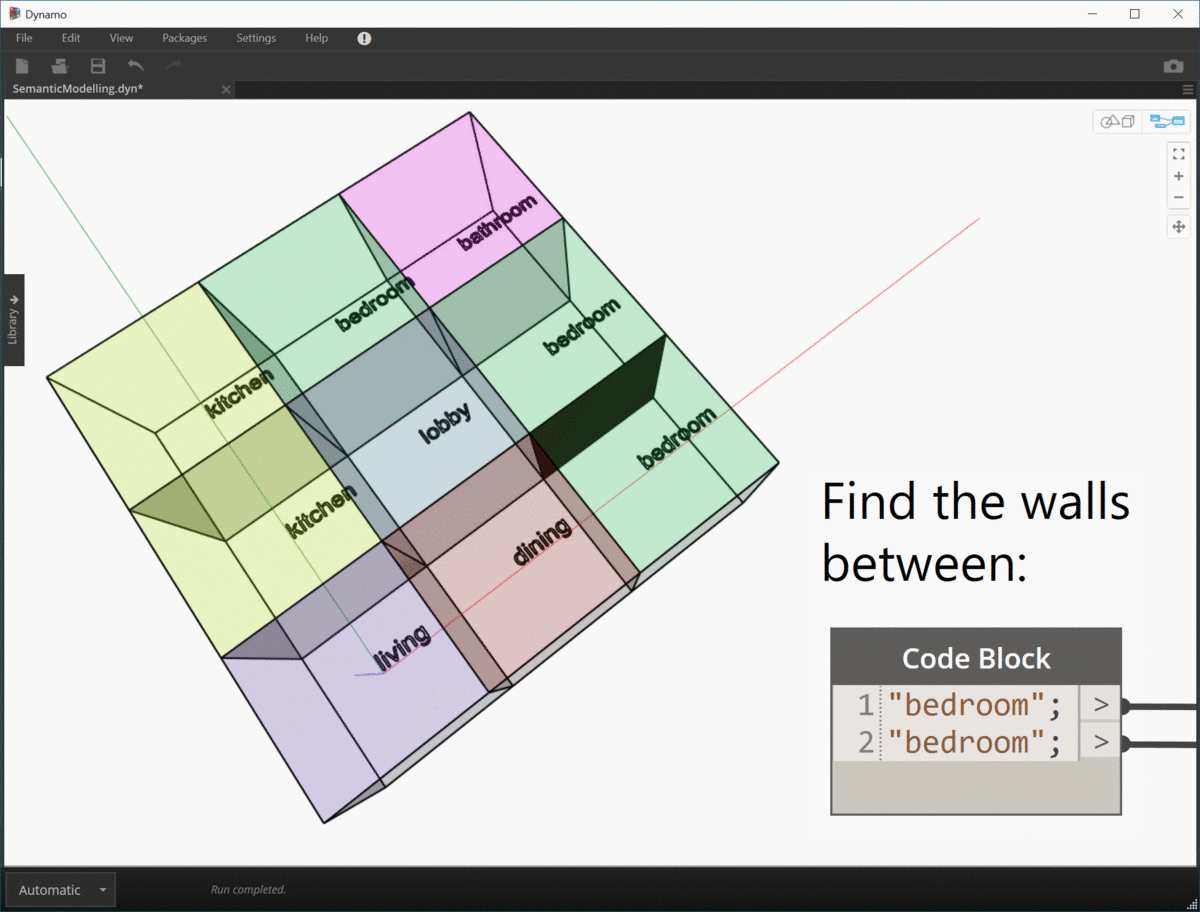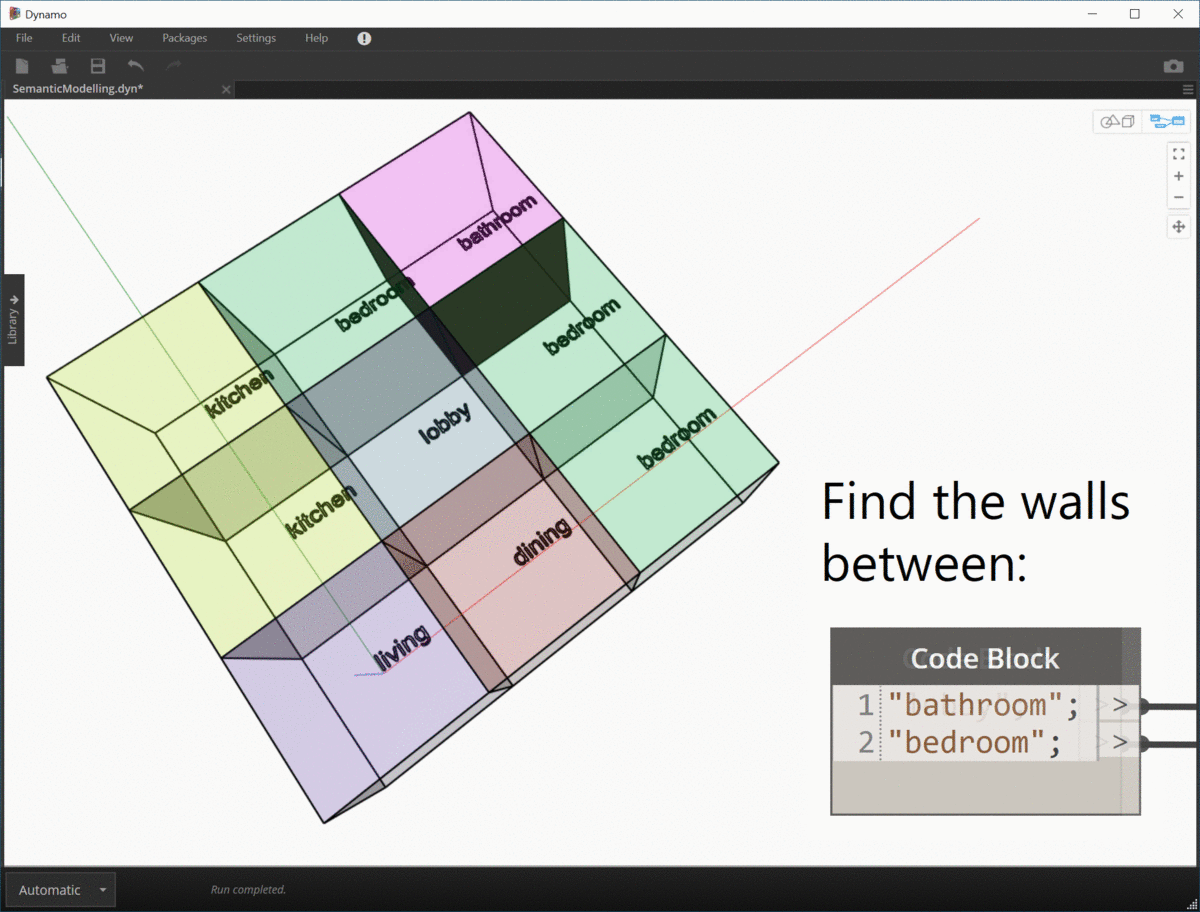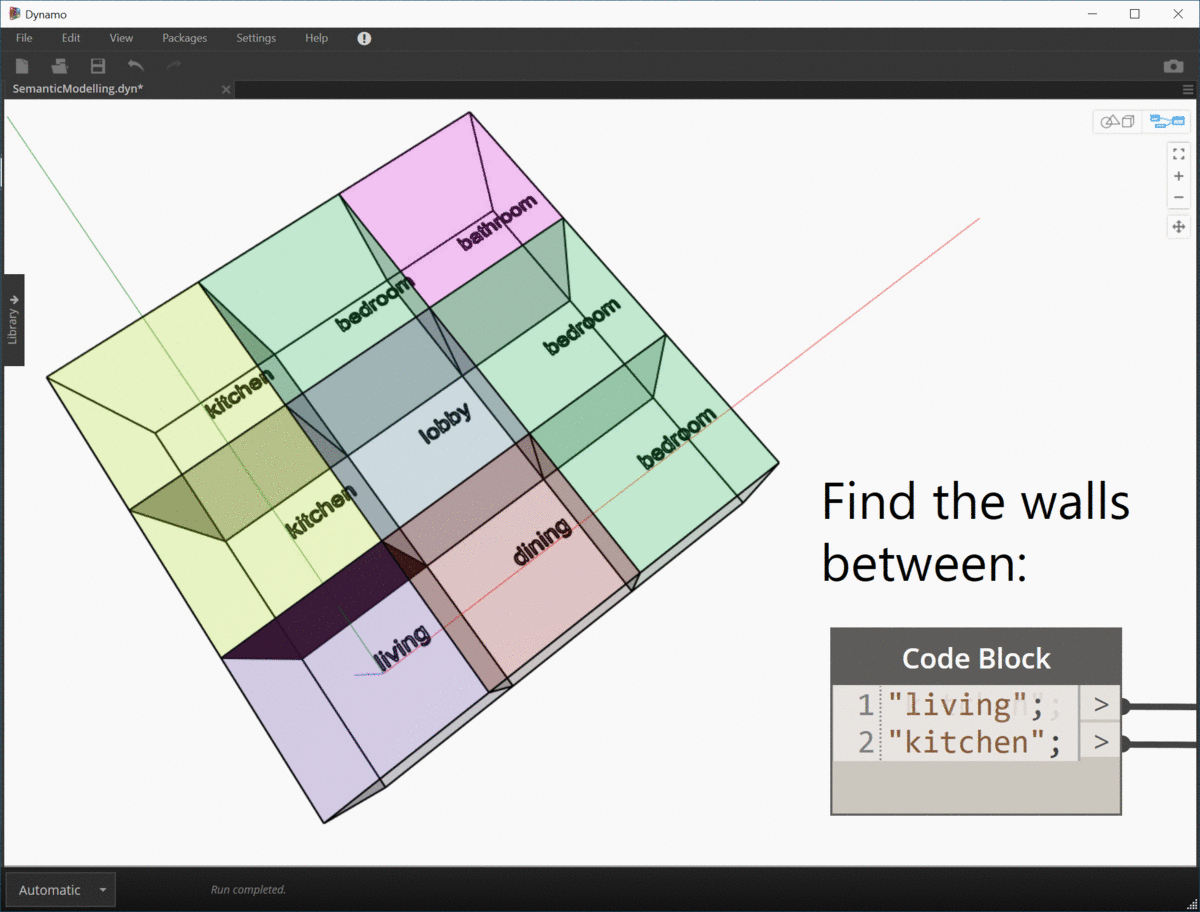
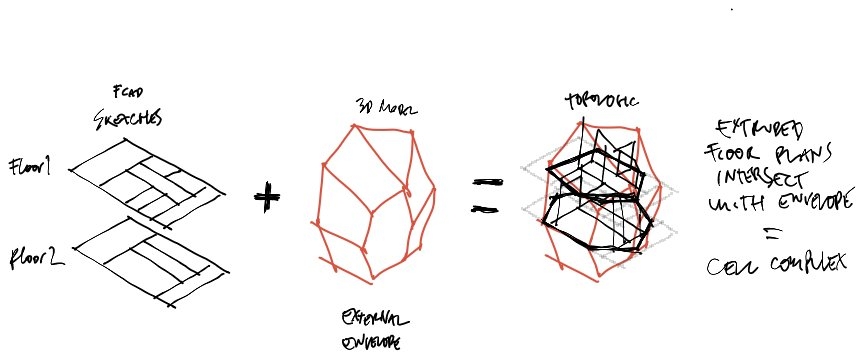
I can't wrap my head around the advantages of graph theory (yet) but the advantage of topologic is that when you add these dictionaries to the whole population of elements, you can after the fact, query the elements (in your case edges that have a certain value on a certain key) and extract a graph.
How I see it is, not only that the graphs are multidimensional but that several overlaid graphs can/could coexist in the same topological construct.
There is where I think the power resides.
Going back to my conceptual background, where I see the power is in that topologic allows/enables us to work on unfathomably complex knowledge structures.
I posit that Christopher Alexander abandoned computation in his research because he realized they couldn't cope yet with the complexity (A city is not a tree (it is a lattice/network) and resorting to "Patterns" that are indeed VERY high level of abstraction objects).
BUT NOW we have the computation power and the tool to deal with them.
@topologic said:
Thanks @paullee. I have heard of that problem in FC, but have not looked deeply into it. This needs testing but here are my thoughts on how this can be avoided. In Topologic you can create Cells, add Dictionaries to them and THEN build a CellComplex. If the original cells do not intersect, the dictionaries transfer 1:1. If the Cells intersect, the new Cells get a new dictionary which contains the values from both parents (e.g. “name”:[“living”,”kitchen”]) So the name of a Cell is not associated with a row number of a cell in a cell complex. There is no guarantee on the order or number of cells created in a CellComplex (eg the Topologic logo starts with two Cells, but creates three Cells when we build the CellComplex)
That would happens probably right? :)
Say, one make a 2d Sketch representing a simple spatial disposition / floor plan. Let Topologic to do some analysis, spatial, energy etc., then feedback to refine the 2d Sketch with some wall orientation to minimise insolation, cut a few window opening to capture some view. Worse still the disposition of rooms swapped, the whole form elongate / rotate. OCCT in FC would possibly return the update Edges/Faces/Solid/Cell reference different from the original models etc. etc. And those 'corresponding cells' just do not intersect.
I fails to compile the codes in the gitHub. Maybe someone can try alterate the 9 Cells in the demonstration to see if there is some similar issue to tackle?
Seems quite some peoples are interested in this library, hope we can start building something in FC :D
What @arquitextonica is hinting at and what I failed to articulate well during the meeting is that because Topologic was created by architects and designers, it frames the knowledge structures in ways that are compatible with design thinking and not necessarily computational thinking. On many occasions while developing Topologic we would ask ourselves: Is this what the user would expect to get? A simple example are the edges of the CellComplex. We could’ve asked each Cell in the CellComplex to give us its faces and each face to give us its wire and each wire to give us it edges. That is computational recursive thinking. But a designer would expect the clean list of unique edges that are the constituent members of the CellComplex.
@arquitextonica
! I don't care about your nonsense comments
I mentioned that type of graphs, because they are popular today, but not in "average" solutions
@JQL As far as I see in this picture you referred to "layered" graphs, graphs that are in different layers and have relations with other upper and lower graph layers too
! However, I understand that for many of you these things are too advanced, and out of your knowledge and experiences :)
@JanF said:
I thought we agreed on using edit with the spoiler tag:
! Hidden text
deleting is appropriate first when someone is actively trolling in my opinion.
You're right, that it what we've agreed, sorry. That 'spoiler' is the function is was looking for, so thanks for the example I could look at to see how it works. It's got nothing to do with moderation I can see, but it's useful. I found out how to restore the posts so now I've just hidden the offensive parts of @ReD_CoDE s text.
@ReD_CoDE anytime you want to have a discussion about how to consistently contribute constructively - there are plenty of people here happy to give feedback if you ask.
@Sabufrancis is this all something that makes sense to your approach?
@duncan I'm not active in BlenderBIM community, because I think I'm in the wrong room, these guys need 3-5 years time to understand my comments
You definitely amaze us with your comments!
@JanF said:
Can we put the recording to the osarch YouTube channel or do you have your own? We'll just share it in that case.
Just general info here - there are playlists on our youtube channel which can be useful for this type of thing. If anyone has a clearly defined theme that is missing as a list of videos then we can bring videos together by making more playlists. For now there are just a few.
Hi everyone. I am looking for beta testers for Topologic for sverchok on Linux. Anyone willing to test, please contact me. Thanks.
The zip file is available at http://github.com/wassimj/topologicsverchok
Login or Register to reply.
